Click on the small pictures below for four views of a 3-dimensional Investment Opportunity Set, drawn for three assets, each of whose returns has a stable distribution with alpha = 1.8, but different values of the location parameter delta, the scale parameter c, and the skewness parameter beta. See discussion below.
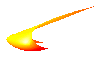 3-D View
3-D View
 Side view, from -beta direction.
Side view, from -beta direction.
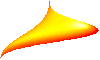 Front view, from -c direction.
Front view, from -c direction.
 Top View, from +delta direction.
Top View, from +delta direction.
Discussion
The three assets shown have stable parameters (alpha, beta, c, delta)
equal to
If all assets had the same skewness parameter beta, or if investors were indifferent to skewness, the side view from the -beta direction would be the relevant IOS, and 2-fund separation would work in the usual manner. However, investors will not ordinarily be indifferent to beta, some being more or less tolerant of negative skewness, and some more or less attracted by positive skewness. Two fund separation is therefore not applicable in this case. There is probably some kind of three-fund separation theorem that applies, but I have not yet worked this out. These figures merely help visualize the problem.
In these figures, the risk-free asset will be represented not by a single point, but by a line (offscale) at c = 0, with delta = Rf, and running across all values of beta. When c = 0, beta has no effect, and therefore investors will be indifferent to it. Mixing Rf with any risky portfolio A on the IOS will generate portfolios lying on a straight line from this risk-free locus to A, all with the same value of beta as A. At worst, investors will therefore face a ruled market surface consisting of an infinite number of straight lines from the Rf locus to tangencies with the IOS at the same beta value. This surface will be curved downward in the beta direction, as is obvious from the figures.
There may be some additional kind of synthetic asset, resembling a call on the market portfolio, that, together with Rf and the market portfolio, spans a superior set of returns. I do not yet see how to keep these returns closed within the set of skew-stable distributions, however, since a call on the market would not itself have precisely a skew-stable return.
With only 3 assets, the skew-stable IOS is a shell that constitutes its own Investment Opportunity Frontier, much as in the Gaussian case when there are only 2 assets. With 4 or more assets, the skew-stable IOS will in general have volume. The IOF will then be the minimal scale subset of this volume, but may still have the qualitative shape of the IOF shown in these figures.
See my paper, "Financial Applications of Stable Distributions," in GS Maddala and CR Rao, eds, Statistical Methods in Finance , Handbook of Statistics , vol. 14 (1996), for further information on stable distributions in finance, and extensive references.
These figures were generated in MATLAB 4.0, by generating a 100x100 grid of portfolios with different mixtures of the 3 assets, and plotting these with SURFL. I played around with the light source direction until it showed the shape of the surface well. COLORMAP(HOT), used here, shows up nicely on a black background, while COLORMAP(COPPER) prints out nicely on white paper. Click here for the source MATLAB M-file .
If the full-screen figures do not fit on your screen, and you are using Netscape, try deselecting SHOW TOOLS, SHOW DIRECTORY BUTTONS, and/or SHOW LOCATION on the OPTIONS menu. If you have deselected BUTTONS, return to this page using the GO menu.
Return to top of this page.
Return to JHM home page.
This page maintained by J. Huston McCulloch, at
mcculloch.2@osu.edu
Page last revised 4/29/99.